이번 주부터
이진 트리의 최대 깊이에 대해 이야기하겠습니다.
설명은 다음과 같습니다.
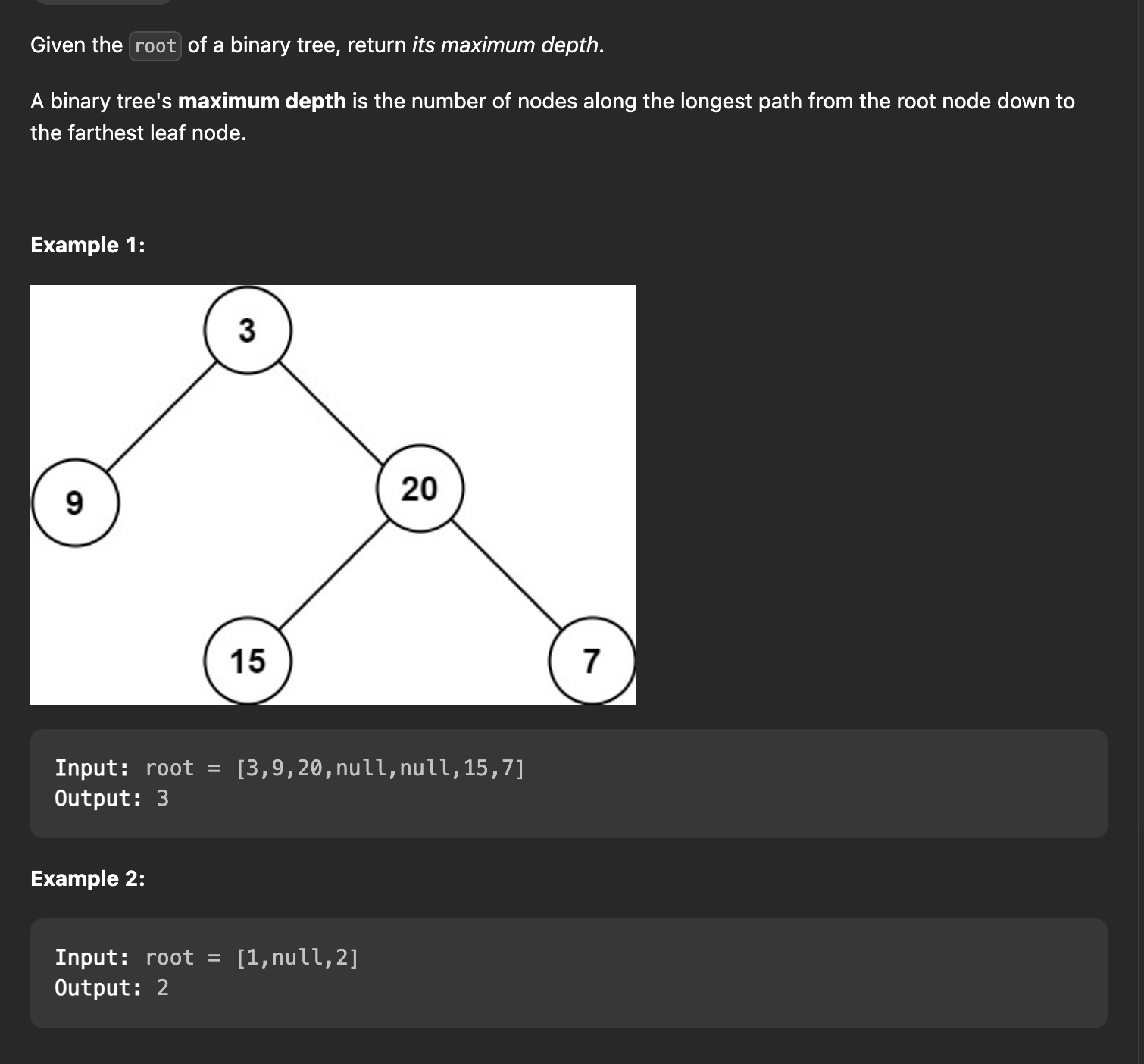
그것은 간단합니다. 우리는 이진 트리의 깊이를 얻으려고 노력하고 있습니다. 예 1은 “3”을 반환하고 예 2는 “2”를 반환해야 합니다. 이 문제를 어떻게 해결합니까?
재귀를 사용하는 솔루션은 다음과 같습니다.
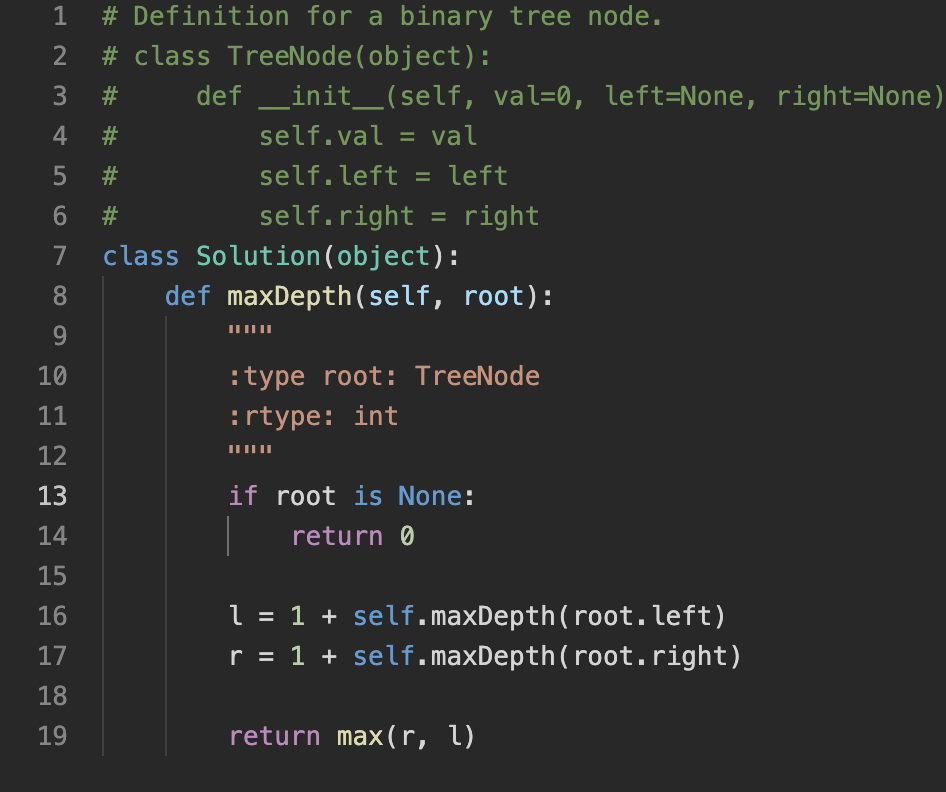
이것은 재귀를 사용하는 방법입니다. 트리를 내려가서 트리의 깊이에 1을 더합니다. 재귀 함수에는 l과 r이 모두 있으므로 어느 것이 더 긴지 비교해야 합니다. 따라서 max(r, l)을 사용하여 트리의 깊이를 비교합니다. 시간 복잡도는 O(N)이고 공간 복잡도는 O(N)입니다.
다음은 이진 검색 트리를 사용하는 또 다른 방법입니다.

q가 큐이고, 레벨이 트리의 깊이를 가리키는 포인터라고 합시다. 큐가 있고 하위 노드를 큐에 추가하려고 합니다. 예제 1에서 우리는 3이 하위 노드(9, 20)를 가지고 있음을 발견했습니다. 하위 노드를 추가한 후 레벨에 1을 추가합니다. 포인트 3에서는 1이 됩니다. 이 솔루션의 시간 복잡도는 O(N)이고 공간 복잡도는 O(N)입니다.
